Un saber generado por investigación interdisciplinar mediante modelización matemática, en su capa más exterior, no es conocimiento calificable de matemático; al situarlo en la balanza fáctico-formal esta se inclina hacia el platillo disciplinar, el atingente al realismo. Además las disciplinas no matemáticas concurrentes cuentan a su favor con varios aspectos prácticos, e. g., aventajan en capacidad de comunicar al gran público sus avances y conclusiones respecto de un fenómeno bajo estudio. En efecto, al indagar en problemáticas propias de ciencias no del todo matematizadas (como la biología) el modelizador ha de reconocer que el protagonismo se ubica en lo fáctico, el contexto que define: la intención del modelo, en gran medida los utensilios y el relato conclusivo; esto último a través de registros figurativos y un lenguaje cercano al natural, más cómodo y de alcance mayor, digamos donde Mathema no llega.

Al observar la presencia de las matemáticas en experiencias de investigación interdisciplinar resalta principalmente que estas tienen un rol metodológico. En este sentido, es importante que los agentes modeladores, en favor de su arte, conozcan y articulen las diferencias ontológicas y epistemológicas existentes entre los elementos propios de la matemática, que dan cuenta de su ser y potencial, con las correspondientes formas y métodos de validación empíricos de las ciencias naturales. El configurarse una panorámica y nivel de pronunciamiento sobre estas disimilitudes, es un mínimo exigible a un modelador matemático; es la pretensión de esta editorial, sin más afán de compartir un informal asomo al tema.

EL ESPACIO INTERDISCIPLINAR

La investigación en matemáticas conlleva una presunción, otorgarle a los elementos en análisis cierto estatus de realidad objetiva. Ante un desafío de la especialidad, el hacedor de matemática, con sentido estratégico, combina y le da existencia a sus entidades ideales por medio de reglas de deducción prestablecidas, un tipo de juego híper regulado y complejo, por lo general, socialmente inocuo. A veces, un dramático soliloquio en un conflicto autoimpuesto o presentado por pares de la cofradía temática. Sin embargo, cuando el desafío-problema no es entidad abstracta y matemática, sino que está mediado por una disciplina de orden fáctico, para el matemático aplicado establecer su juego acostumbrado pasa por sumar una complejidad diferente, pues deja de ser preestablecido y totalizador en cuanto a tipos de objetos, reglas y consecuencias. Además, suelen emerger límites a las expectativas del equipo y aristas de subjetividad, potencialmente paralizantes para el modelizador novato.

Dentro de un equipo de investigación interdisciplinar, a la presentación de una situación problema en el lenguaje de una ciencia de contexto no matematizada y ad hoc al fenómeno bajo observación, debe seguir un proceso de adaptación y reordenamiento de perspectivas y un consenso del plano de la comunicación formal del equipo. Nos referimos a una serie de elementos técnicos y también prácticos que de quedar bien o mal instalados, pueden llegar a determinar el éxito o fracaso del equipo. Aunque, siendo estos elementos importantes, existen otros de profundidad filosófica, por ejemplo, el rol epistemológico reservado a la matemática, también ineludibles para el modelador especializado que busca entender su quehacer.

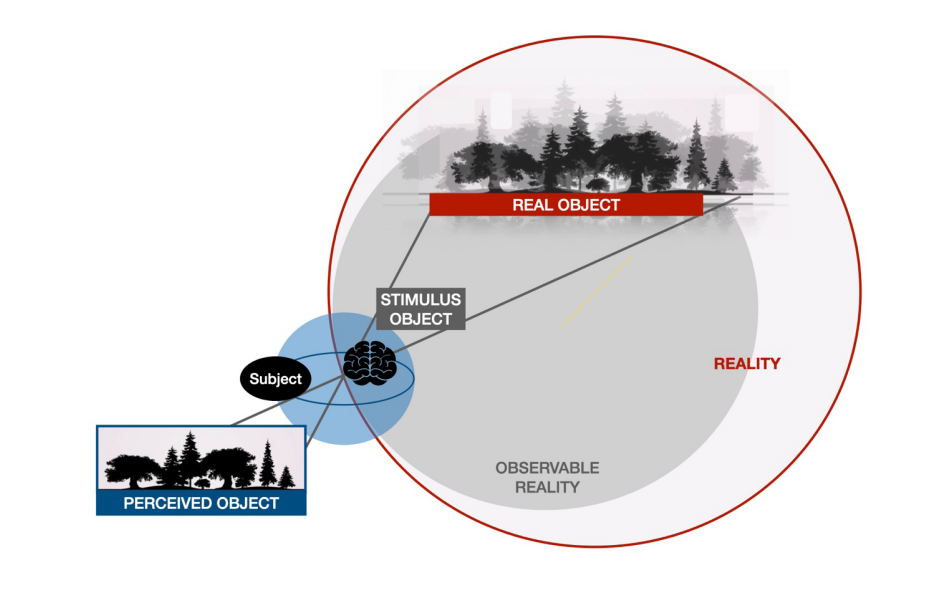
Figura 1. Relación sujeto y sus objetos asociados: objeto-real (cosa en sí), objeto-estímulo (como unidad sensorial) y objeto-percibido (mediado y registrado por la consciencia). Existe una perspectiva intencionada sobre el objeto-real que está
en coevolución con la historia de vida del objeto-percibido en el sujeto.

En contraste al espacio de trabajo idealizado y convencionalmente determinado con que cuenta un laborioso instalador de teoremas con sus respectivas pruebas lógico-matemáticas, el modelador recibe y reacciona ante un fenómeno-problema (natural o social) a través de procesos helicoidales de abstracción, análisis e interpretación. En estos, las sucesivas puestas en símbolos y relaciones matemáticas de los configurantes son actos inseparables de sus pretendidas transducciones semánticas. Comenzará por lo ya conocido de estas realidades y por el alcance de las preguntas de investigación del equipo investigador. Un modelo, como posibilidad de objeto matemático, llevará la indeleble y decantada marca de lo que son las percepciones contingentes, históricas y anhelos que los investigadores concurrentes tienen sobre el trozo de realidad bajo la lupa. En su tarea, el modelador para optimizar su rol en la investigación interdisciplinar, está llamado a explorar la intersubjetividad en pro de una comunicación efectiva. Notemos que en este hacer científico, está en valor quien se adapta a la idea de cognición compartida y al logro permanente de consensos, pues resulta esencial para la renovación de las ideas. La investigación científica vía equipos interdisciplinarios es un acto dialógico, que parte por el reconocimiento de la percepción y las formas de las otredades disciplinares en cuánto a la naturaleza de los modos de situar los objetos de investigación y los métodos de elaboración de certezas involucrados.

DIFERENCIACIÓN ONTOLÓGICA

Un sujeto intencionado frente a un espacio de observación sensible o psíquico busca el reconocer o dar forma a un pedazo o trama de tal existencia. Así, ante el emerger de unas primeras líneas de borde que aprecie de interés, tiende a desplegar su facultad biológica de obtener un recorte más estable; aplica sus tijeras mentales para generar una impresión con la que posteriormente juzgará adaptativamente sus experiencias futuras. Si sistematiza, logra fijar y penetrar en lo que a otros les es efímero e inexpugnable, capturando cierta unidad identificable, e. g., lo que es la idea de bosque desde el paisaje, ver Figura 1. Así, el sujeto ha dado forma a lo que denominamos objeto percibido; un recorte por lo general plástico y dinámico. Este objeto percibido tiene un conjunto de posibilidades de realización, o estados, en conexión con otros objetos y el mismo sujeto, y se presenta siendo parte de sistemas de objetos, una suerte de fotografías identitarias factibles.

Los estados de un objeto son en general inestables, proclives a cambios por estímulos naturales o por intervención. Unos estados, los causales, llevan necesariamente o hacen pasar al objeto a un estado sucesor, el estado efecto, y no así a otros que son independientes. En este sentido, si un estado es una fotografía, los estados derivados en orden temporal conforman un proceso, es decir, definen un trayectoria. Así, visualizamos historias de vida de los objetos como filmes cinematográficos factibles, lo que en sistemas dinámicos llamamos órbitas. Los determinantes de la trayectoria de un objeto percibido, los desarrolladores de su guion específico, están dados por la acción conjunta de conexiones subyacentes a la estructura de la realidad-experiencia, una arquitectura de relaciones (leyes), que para no caer en rigidez determinista, podemos también admitir vibrante.

Hay necesidad de identificar al interior del espacio de existencia del objeto y su historia (realidad) el subespacio de sus representaciones. En el mundo de los hechos, lugar de interacción y transformación de los objetos en sí, distinguir el lugar que tenemos para referenciarlos y pensarlos; sea con óptica de disciplina de contexto o la del idealismo matemático. En este sentido, consideramos adecuado reservar para los objetos y hechos de la realidad el principio de identidad concreta de la ontología dialéctica, que permite pensar las trayectorias del objeto-percibido como la unidad que se diferencia y desdobla. Mientras que reservamos el principio de identidad abstracta de la lógica matemática para los objetos y sistemas referenciales ideales. Al respecto, puntualicemos que un objeto percibido es unidad en cuanto lo que es observado es alguna característica general y se desdobla por aquellas características más particulares, una separación que un objeto matemático afortunadamente no presenta. Notemos que “en el proceso de la cognición idealizar y simplificar la realidad, en ciertas condiciones, no sólo resulta posible, sino incluso necesario” (Identidad en Diccionario Filosófico, Rosental-Iudin). Quien modela debe estar consciente que la dualidad abstracto-concreto es una llave permanente para entender y desarrollar los actos tendientes a generar conocimiento de los objetos en algún aspecto específico deseado, en que responder ¿qué se abstrae y qué no del objeto-percibido? es la vía para llegar a alcanzar saberes respecto de lo concreto. Destaquemos también que a un modelador le viene cómodo tener a la propia lógica como modelo abstracto de las relaciones causa-efecto del lenguaje natural.

¿Qué bases tenemos para sostener la esperanza de conocer, de alcanzar conocimiento a través de un proceso de modelización? ¿Dónde radica nuestra confianza? Al respecto, Wittgenstein afirma que el lenguaje es un modelo del mundo, que las cosas del lenguaje son las proposiciones, que las del mundo son los hechos (sistemas de objetos) y que existe una correspondencia entre hechos y proposiciones que refleja en la estructura del lenguaje la del mundo. La matemática, en cuanto lenguaje formal, que permite la argumentación para la derivación argumental, es un camino viable, aspecta muy bien para revelarnos tan íntima arquitectura del mundo. Así, frente a la primera pregunta de toda teoría del conocimiento: ¿Es posible conocer? La respuesta, confiando en el autor del Tratado lógico-filosófico, es afirmativa.

La Figura 2 muestra un paisaje de la realidad en que destaca un arcoíris, el cual en cuanto a recorte de cierto sujeto es un sistema que conecta con la lluvia y el sol, pero ajeno al objeto bosque. Muy probablemente en la experiencia de tal sujeto hay registro de otros arcoíris sin la presencia de bosques. Sin embargo, un sujeto que nunca ha salido de su aldea situada en plena foresta no necesariamente dejaría a éste fuera del registro. Esto sugiere que la experiencia colectiva, como la de un equipo interdisciplinar, suma a las posibilidades de reconocer las conexiones esenciales de aquellas meramente contingentes. Hacemos notar que esta propiedad de la consciencia, de desconectar o conectar percepciones, es un aspecto clave en la investigación vía modelización.

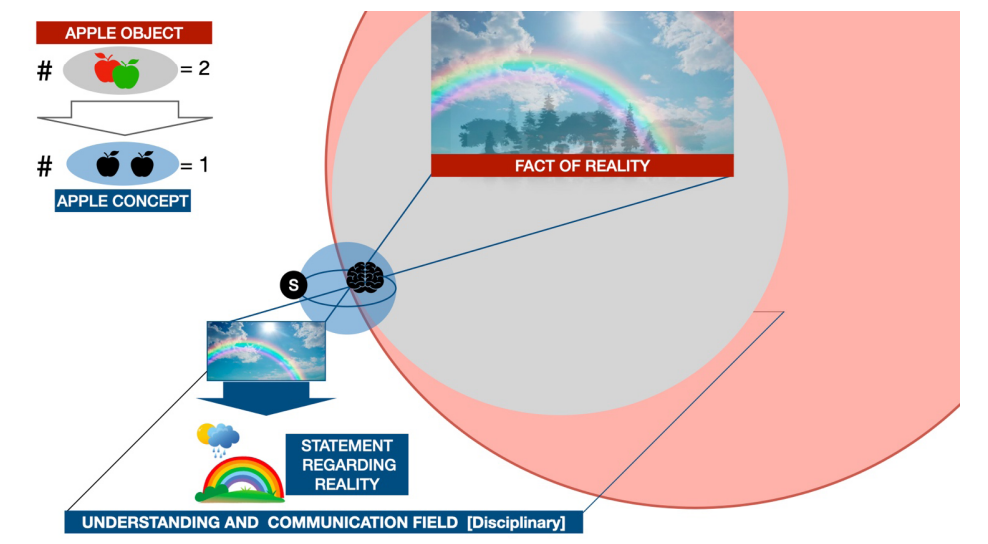
Figura 2. Una comunidad disciplinar registra y proyecta su experiencia sobre rasgos específicos de interés común de los hechos sobre el plano de intelección y comunicación vía conceptos y enunciados. El concepto debe ser único, no hay dos conceptos de manzana, pero sí pares de manzanas. El enunciado conecta conceptos y se juzga como verdadero (o falso) por experimentación.

Dado un hecho existirán tantas perspectivas como sujetos observantes, pero si estos forman una cultura pues tienen regular afán investigativo e intención ontológica semejante, digamos que comparten el set de características de los objetos en que se enfocan y hacen uso de extensiones consensuadas de los sentidos (mismas tijeras), ellos están dando cuerpo a una disciplina de contexto. Estas comunidades científicas hacen registro de la experiencia común y de las proyecciones que determinan (lo representado), lo que en la Figura 2 etiquetamos como plano de la intelección y la comunicación disciplinar. Entonces, un mismo hecho, en cuanto a conexión (o sistema) de objetos de la realidad, puede presentar tantas variantes en cuanto a objeto-estímulo y objeto-percibido, como disciplinas estén interesadas en el hecho en cuestión.

El plano disciplinar es el lugar donde nace y se sitúa cada nuevo concepto científico, modo de rotular a una familia de objetos-percibidos que tienen un patrón reconocido por la experiencia colectiva. Los conceptos, para la consistencia lógica del trabajo con ellos, han de ser únicos (presentar consenso). Con frecuencia ocurre que la palabra asociada con el concepto coincide con la palabra usada para cualquiera de sus representados. En la esquina superior izquierda de la Figura 2 representamos esto, ya que como objetos de la realidad pueden existir dos manzanas, pero nunca dos conceptos manzana. Lo anterior no es dilema para un matemático, pues ante la pregunta por la cardinalidad del conjunto {1/2 ; 0, 5} no duda en responder que es uno, un síngleton, ya que en matemática los objetos son siempre sólo conceptos. Sólo si quien percibe estuviera enfocado en la grafía, esto es, en el significante, modo que está por fuera de la intención matemática, en razón diría que dicha cardinalidad es dos.

Llegamos a un punto en que es necesario distinguir entre los planos de intelección involucrados en el trabajo interdisciplinar. Están los planos de contexto, siendo aquellos en que sus conceptos están directamente ligados con los objetos fácticos de interés de la disciplina. En estos planos (o espacios proyectivos) la unidad fundamental de conocimiento y comunicación es el enunciado, una afirmación que conecta conceptos y que se establece con la intención de justificar el por qué un hecho ocurre o no. Por otro lado, está el plano matemático, en que los conceptos se liberan de su amarre con los objetos de la realidad y pasan a tener un interés en sí mismos, en los conceptos y las relaciones consistentes entre estos; es decir, se convierten en objetos de estudio, objetos de un tipo diferente, vacíos de realidad concreta, técnicamente denominados objetos ideales. En este plano también tenemos los enunciados, que para distinguirlos preferimos llamar proposiciones. En cuanto ambos tipos de planos, el disciplinar y el matemático, involucran lenguaje podemos recurrir al muy conocido triángulo semiótico para puntualizar diferencias entre enunciados y proposiciones que un modelador debe tener en permanente consideración. Como indica la asociación vía colores en la Figura 3, el plano disciplinar está superlativamente orientado a la relación de sus signos con sus referentes, a lo semántico, que linda con el movedizo terreno de la verdad. Por otro lado, en el espacio matemático la orientación del quehacer da cuenta de la consistencia y de las derivaciones lógicas de las proposiciones entre sí; esto es, predomina una perspectiva sintáctica. En este sentido, es posible establecer un paralelismo contrastante entre enunciados y proposiciones, mientras los primeros son objetos conceptuales con semántica exterior, i. e., con referencia a los hechos, los segundos hacen referencia a objetos ideales con una semántica interna y en que la correspondencia buscada es con la razón, a lo que nos referiremos como corrección del pensamiento. Así, la tarea última del modelador en equipos interdisciplinarios es concluir desde el modelo proposiciones derivadas por argumentos correctos, las que interpretadas y en la forma de enunciados, no sólo sean validas, sino que aspiren a ser verdaderas.

DIFERENCIACIÓN EPISTEMOLÓGICA

Respecto de la milenaria disputa de si es la razón o la experiencia la génesis de nuestros saberes respecto del mundo, un modelador en contextos interdisciplinarios alguna claridad habrá de construir para efectos de la convivencia que ha de sostener entre los métodos de su disciplina y los clásicos de las ciencias fácticas. Por ejemplo, en el método hipotético deductivo (MHD) que a grandes bloques asume el flujo: observación, hipótesis y consecuencias contrastables, ¿dónde se ubica el aporte de una modelización matemática? Tener alguna luz es una necesidad que surgirá en la interacción interdisciplinar, esta probablemente se presentará al definir los roles y al evaluar el alcance del aporte formalista.

En las ciencias fácticas el investigador está interesado en consolidar o en innovar en respuestas a ciertas preguntas de investigación y, desde el análisis sobre observaciones previas, levantar una hipótesis, una conjetura contexto-causas-efectos que explique el fenómeno de interés. La hipótesis normalmente se prueba a través de la implementación de diseños experimentales específicos. ¿Qué hace un modelo ante una hipótesis? ¿Un modelo matemático puede llegar a rechazar o aceptar una hipótesis? ¿Las proposiciones matemáticas derivadas tienen con claridad, por interpretación, un relato de verdad como enunciados sobre la realidad?

Al respecto, sobre las contrastaciones leemos: “En este Método (el MHD) las contrastaciones deben ser experimentales. Y deben ser contundentes, en el sentido de que deben decirnos claramente si las consecuencias deducidas de la hipótesis se dan en la realidad o no” (Sobre un concepto histórico de ciencia, Carlos Pérez).

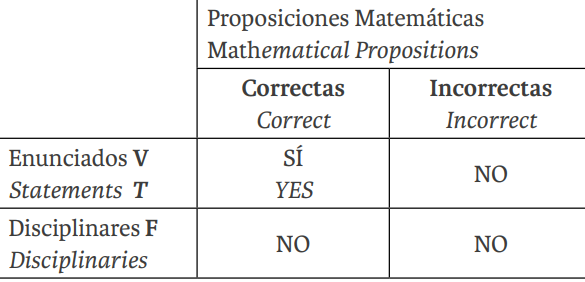
Como ya fue observado, en el trabajo en equipos interdisciplinares concurren el plano proyectivo teórico (el disciplinar) y el plano matemático. Notemos que una hipótesis científica es un enunciado del plano de contexto, por lo que no es un hecho y, en principio, tampoco una proposición matemática, y sólo se vincula con los hechos por referencia. De modo que, entrando al terreno de la verdad, observamos que es en este plano disciplinar donde los enunciados pueden llegar a ser verdaderos o falsos, ya que en el de la realidad, no hacen sentido esos calificativos, pues los hechos ocurren o no (se dan o no se dan). Ahora, respecto del plano de la matemática, es mejor reservarnos otros términos, pues para la comunicación de grupo es prudente referirnos a proposiciones, destacando las que tienen una demostración a distinguir entre el pensamiento deductivo correcto o incorrecto. Así lo deseado es alcanzar enunciados hipotéticos que tienen un correlato matemático como proposición correcta en el paso del antecedente al consecuente y, que además interpretadas pasen la prueba o contrastación empírica para convertirse en verdaderas. Aunque esto último, es sobre la base de resistir un testeo permanente de no falsedad en el campo experimental.

Notemos que, una hipótesis es una apuesta de realidad, es aquel enunciado con algún grado de fundamento y, además, contrastable que, presuponiendo ciertos hechos afirma que necesariamente se deriva otro hecho, generalmente relacionado con la especificación para un objeto-percibido de un estado o un tipo de estados dentro de los factibles. Entonces, si bien el MHD nos habla del contraste empírico a través de la experimentación, también existe el contraste de racionalidad y por ahí surge una primera oportunidad de la modelización matemática, testeando si la hipótesis es lógicamente consistente. Otra posibilidad es modelando las contrastaciones empíricas (v. g., no posibles de implementar), como experimentos mentales, chequeando que sus conclusiones analíticas van (admiten la interpretación semántica) en la dirección de lo que afirma la hipótesis. Sin embargo, un enunciado como la hipótesis, con su generalidad, aún siendo lógicamente consistente, puede llegar a ser un enunciado menos verosímil, nunca se está seguro que aparezca un experimento que le contradiga. Así, ya que la verdad de una hipótesis consistente se juega su verosimilitud en el control empírico, bajando las expectativas los modelos sólo suman o restan argumentos o soporte para su formulación.

Los equipos científicos monodisciplinares suelen estructurar o guiar su plan de trabajo a través de una pregunta de investigación, lo mismo ocurre en los interdisciplinares. ¿Qué tipo de modelo es el adecuado para esta pregunta? ¿Cuáles son las transferencias legítimas desde lo representado hacia el modelo representante (abstracción), e inversamente (interpretación)? ¿Cuáles son los elementos mínimos, primeros y necesarios de considerar, para llegar a construir un modelo con algunas pretensiones analógicas respecto de fenómenos de la realidad con posibilidades de aportar a una respuesta de la pregunta de investigación? Vale tener claridad respecto de la distinción ontológica entre objetos y hechos de la realidad, el lenguaje como articulador de conceptos a través de las proposiciones y el conjunto de objetos ideales y relaciones formales, lo matemático que aspira a convertirse en modelo.

DESPEDIDA

Al modelar no sólo debemos estar conscientes de las diferencias entre contexto y matemática respecto de objetos, proposiciones declarativas y métodos involucrados, hay muchos otros aspectos con trazas filosóficas que un modelador puede explorar para una mejor comprensión de su labor. Un enorme espacio que tienta al afán exploratorio, es el sentido de valor que involucra la tarea, sea el de uso y, por qué no, también el estético, pero esta editorial ya se ha alargado demasiado.

Finalizo apuntando que ante una pregunta de investigación, su hipótesis asociada y un nivel de precisión de la respuesta, aparte de lo ya expuesto, es útil y bello que el modelador aspire a construcciones que realicen la tarea en la forma más simple posible, vale aquí para esta y otras temáticas recomendar el libro Deja a la estructura hablar: modelización y análisis de sistemas naturales, sociales y socioecológicos, del doctor Rodrigo Ramos.

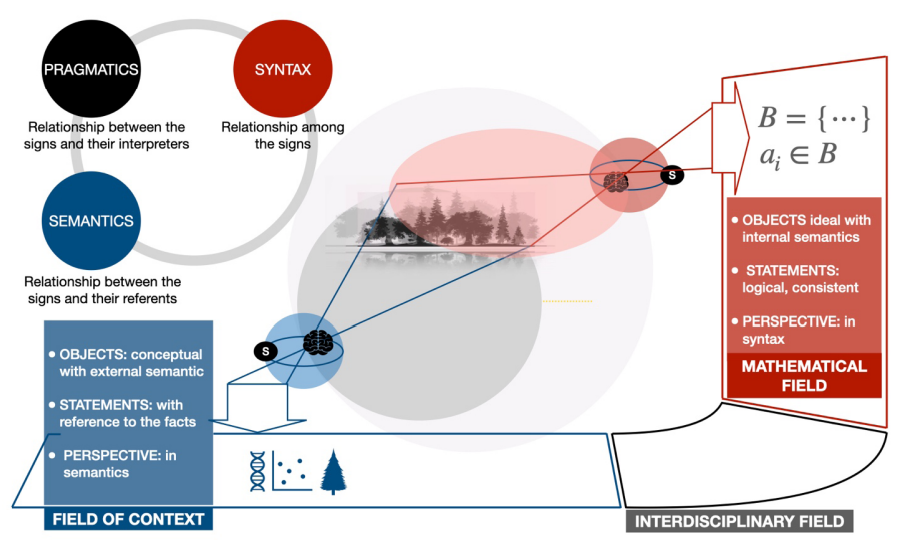
Figura 3. En el plano contexto, el enunciado tiene significación en los hechos; su semántica es exterior, se da o no en sus referentes reales. En cambio, en las proposiciones matemáticas, los referentes son solo conceptos, objetos-ideales, una semántica interna; resalta la sintaxis, la relación de los signos entre sí. La interacción va definiendo por adaptación el plano interdisciplinar de comunicación en el que conviven enunciados de contexto y proposiciones matemáticas. En cuanto a la pragmática, tercer vértice semiótico, es preocupación de otros planos imaginables, e. g., los conectados con la psicología o las ciencias de la educación.