Knowledge generated by interdisciplinary research through mathematical modeling, in its outermost layer, is not knowledge that can be classified as mathematical. When placing it in the factual-formal balance, it leans towards the disciplinary dish, the one related to realism. In addition, the concurrent non-mathematical disciplines have several practical aspects in their favor, e. g., they have an advantage in the ability to communicate to the general public their progress and conclusions regarding a phenomenon under study. Indeed, when inquiring into problems typical of sciences that are not completely mathematized – such as biology – the modelers should recognize that the leading role is located in the factual side, i.e., the context that defines: the intention of the model; to a large extent the utensils; and the concluding story. The latter is performed by means of figurative registers and a language close to natural, which should be more comfortable and have a greater scope, let’s say where máthēma does not reach. Observing the presence of mathematics in interdisciplinary research experiences mainly highlights that it has a methodological role. In this sense, it is important that modeling agents, in favor of their art, know and articulate the ontological and epistemological differences existing between the mathematical elements, characterized by their being and potential, with the corresponding forms and methods of empirical validation of the natural sciences. Configuring an overview and level of pronouncement on these dissimilarities is a minimum required from a mathematical modeler, which is the goal of the present editorial, with no further desire than sharing an informal glimpse of the topic.
THE INTERDISCIPLINARY SPACE
Research in mathematics entails a presumption, granting the elements under analysis a certain status of objective reality. Faced with a challenge from the specialty, mathematicians, with a strategic sense, combine and create their ideal entities by means of pre-established deduction rules. It is a type of hyper-regulated and complex game, generally socially innocuous. Sometimes, it is a dramatic soliloquy in a self-imposed conflict or presented by thematic brotherhood peers. However, when the challenge-problem is not an abstract and mathematical entity, it is mediated by a discipline of a factual order. The applied mathematicians can establish their usual game by adding different complexities, since they are no longer pre- established and totalizing types of objects, rules and consequences. In addition, limits to the expectations of the teams and edges of subjectivity tend to emerge, potentially paralyzing for novice modelers.
Within interdisciplinary research teams, the presentation f a problem situation in the language of a non-mathematized science context and ad hoc the phenomenon under observation should be followed by a process of adaptation and reordering of perspectives and a consensus on the field of formal team communication. We are referring to a series of technical and also practical elements that, if well or badly established, can determine the success or failure of the teams. Although these elements are important, there are others of philosophical depth-e. g., the epistemological role reserved for mathematics-also unavoidable for specialized modelers who seek to understand their work.
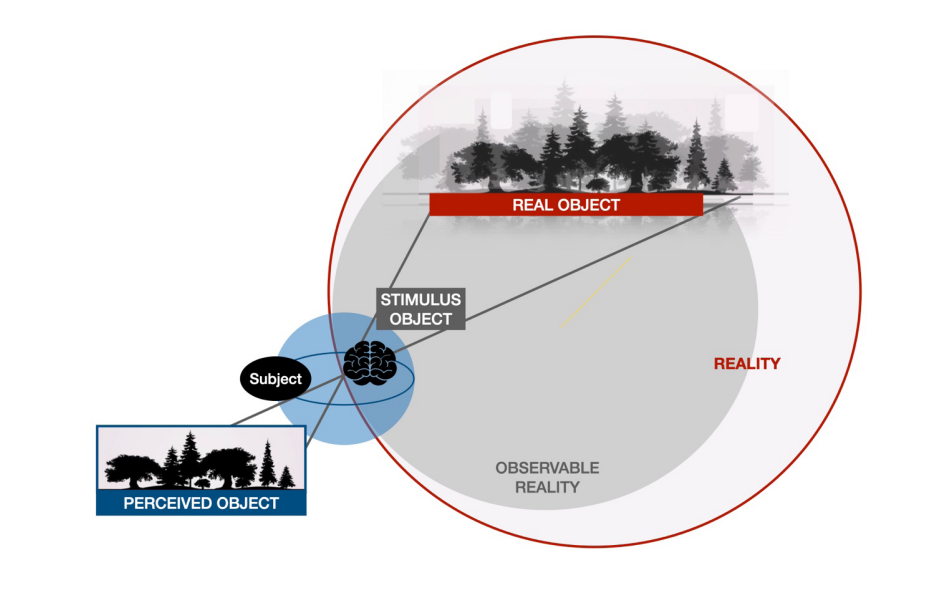
Figure 1. Relationship between subjects and their associated objects: real object (thing in itself); stimulus object (as a sensory unit); and perceived object (mediated and registered by consciousness). There is an intentional perspective in the subject with respect to the real object that is in coevolution with the life history of the perceived object.
In contrast to the idealized and conventionally determined workspace available to laborious installers of theorems with their respective logical-mathematical proofs, modelers receive and react to a phenomenon-problem (natural or social) through helical processes of abstraction, analysis and interpretation. In these processes, the successive putting into symbols and mathematical relationships of the shaping elements are actions that cannot be separated from their alleged semantic transductions. Modelers will begin with what is already known about these realities and with the scope of the research questions of the research teams. A model, as a possibility of a mathematical object, will bear the indelible and distinguished mark of the contingent and historical perceptions and desires that researchers have about the piece of reality under magnifying glass.
In their tasks, the modelers are called to explore intersubjectivity in favor of effective communication in order to optimize their role in interdisciplinary research. It is worth noting that, in this scientific practice, those who adapt to the idea of shared cognition and the permanent achievement of consensus are valuable, since these aspects are essential for the renewal of ideas. Scientific research via interdisciplinary teams is a dialogical action. It begins with the recognition of perception and the forms of disciplinary otherness in terms of the ways of situating the research objects and the methods for elaborating certainties.
ONTOLOGICAL DIFFERENTIATION
Determined individuals facing sensitive or psychic observation spaces seek to recognize or shape pieces or plots of such existences. Thus, in view of the emergence of some first border lines that they consider of interest, they tend to deploy their biological faculty to obtain a more stable cutout. They make use of their mental ‘scissors’ to generate an impression with which they will later adaptively judge their future experiences. If they systematize, then they can focus on and penetrate what is ephemeral and impregnable to others, capturing a certain identifiable unity, e. g., the idea of forest from the landscape (Figure 1). Thus, the individuals have given shape to what we call the perceived object, which is generally a plastic and dynamic cutout. This perceived object has a set of functioning possibilities or states, in connection with other objects and the same individuals. It appears as part of object systems, a sort of feasible identity photographs.
The states of an object are generally unstable, prone to changes by natural stimuli or by intervention. Some states, such as the causal ones, necessarily lead or make the objects pass to a successor state, i.e., the effect state, and not others that are independent. In this sense, if a state is a photograph, the states derived in temporal order create a process, i.e., they define a trajectory. Thus, it is possible to observe the life histories of the objects as feasible cinematographic films, which in dynamical systems we call orbits. In the determinants of the trajectory of a perceived object, the developers of its specific script are given by the joint action of connections underlying the structure of reality-experience, an architecture of relationships (laws), which, in order not to fall into deterministic rigidity, can also be considered vibrant.
There is a need to determine the inner existence space of the object and its history (reality), the subspace of its representations. In the world of facts, place of interaction and transformation of the objects, we should determine the place we have to reference and think about them; be it from the optics of the field of context or that of mathematical idealism. In this sense, we consider it appropriate to reserve the principle of concrete identity of dialectical ontology for the objects and facts of reality, thus allowing us to think about the trajectories of the perceived object as the unit that differentiates and unfolds. On the other hand, we reserve the principle of abstract identity of mathematical logic for ideal referential objects and systems. In this regard, it should be highlighted that a perceived object is a unit, whereas what is observed is some general characteristic unfolded by those more particular characteristics, a separation that, fortunately, is not observed in a mathematical object. It should be noted that “in the process of cognition, idealizing and simplifying reality, under certain conditions, is not only possible, but even necessary” (Identity in Diccionario Filosófico [Philosophical Dictionary], Rosental-Iudin).
Who models should be aware that the abstract-concrete duality is a permanent key to understand and perform the actions tending to generate knowledge about the objects in some specific desired aspect, in which answering what is abstracted and what is not from the perceived object is the way to reach knowledge regarding the concrete dimension. It is also worth emphasizing that it is convenient for a modeler to have logic itself as an abstract model of the cause-effect relationships in natural language.
What bases do we have to sustain the hope of knowing, reaching knowledge through a modeling process? Where does our trust lie? In this regard, Wittgenstein affirms that language is a model of the world, that the things of language are propositions, that those of the world are facts (object systems) and that there is a correspondence between facts and propositions reflected in the structure of the language of the world. Mathematics, as a formal language, which allows argumentation for the argumentative derivation, is a viable way. It is adequate to reveal such an intimate architecture of the world to us. Thus, facing the first question of any theory of knowledge: Is it possible to know? The answer, trusting the author of the Logical-philosophical Treatise, is affirmative.
Figure 2 shows a landscape of reality in which a rainbow stands out, which in terms of cutting a certain subject is a system connected to the rain and the sun, but alien to the forest object. Most likely, in the experience of such a subject, there should be records of other rainbows without the presence of forests. However, subjects who have never left their villages located in the middle of forests would not necessarily leave them out of the records. This fact suggests that the collective experience, such as that of interdisciplinary teams, adds to the possibilities of recognizing the essential connections of those experiences that are merely contingent. It should be noted that this property of consciousness that disconnects or connects perceptions is a key aspect in research via modeling.
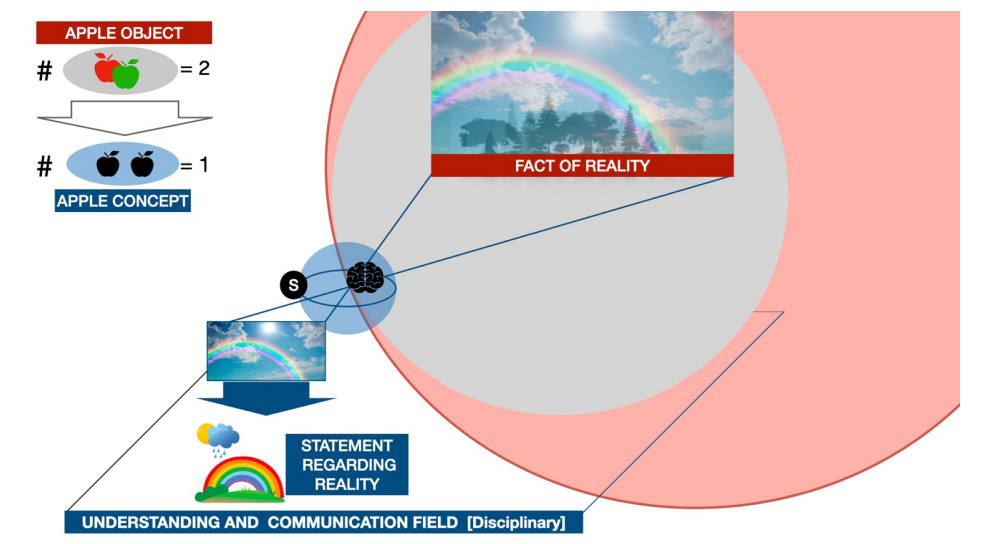
Figure 2. A disciplinary community registers and projects its experience related to specific features of common interest of the facts in the field of intellection and communication via concepts and statements. The concept should be unique, there are not two apple concepts, but pairs of apples. The statements connect concepts and are judged true (or false) by experimentation.
Given a fact, there will be as many perspectives as observing subjects. However, if they form a culture, because they have a regular investigative zeal and a similar ontological intention, i.e., they share the set of characteristics of the objects on which they focus and make use of consensual extensions of the senses (same scissors), they will be giving body to a discipline of context. These scientific communities record common experiences and the projections that they determine (what is represented), what in Figure 2 we labeled as the field of intellection and disciplinary communication. Then, the same fact-in terms of connection (or system) of objects of reality-can present as many variants in terms of stimulus object and perceived object as disciplines are interested in the fact in question.
The disciplinary field is the place where each new scientific concept is born and located, a way of labeling a family of perceived objects that have a pattern recognized by collective experience. For the logical consistency of the work with concepts, they should be unique (exhibit consensus). It frequently happens that the word associated with the concept coincides with the word used for any of its represented factors. In the upper left corner of Figure 2, we represent this fact, since two apples can exist as objects of reality, but never two apple concepts. This is not a dilemma for mathematicians, since when asked about the cardinality of the set {1/2; 0.5}, they do not hesitate to answer that it is one, a singleton, since objects are always only concepts in mathematics. Only if the observers were focused on the spelling, i.e., on the signifier, a way that is outside the mathematical intention, would he reasonably say that that cardinality is two.
We have reached a point where it is necessary to distinguish between the fields of intellection involved in interdisciplinary work. There are the context fields, being those in which their concepts are directly linked to the factual objects of interest of the disciplines. In these fields (or projective spaces) the fundamental unit of knowledge and communication is the statement, an affirmation that connects concepts and that is established with the intention of justifying why an event occurs or not. On the other hand, there is the mathematical field, in which the concepts are released from their connection with the objects of reality and begin to have an interest in themselves, in the concepts and the consistent relationships between them. This way, they become objects of study, objects of a different kind, void of concrete reality, technically called ideal objects.
In this field, we also have statements. In order to distinguish them, we prefer to use the term propositions. The two types of fields, the disciplinary and the mathematical, involve language; however, we can resort to the well-known semiotic triangle to point out differences between statements and propositions that modelers should take into permanent consideration. As the association via colors in Figure 3 indicates, the disciplinary field is superlatively oriented to the relationship of its signs with their referents, to the semantic factor, which borders on the shifting terrain of truth. On the other hand, in the mathematical space, the orientation of the tasks manages the consistency and logical derivations of the propositions among themselves, i.e., a syntactic perspective predominates. In this sense, it is possible to establish a contrasting parallelism between statements and propositions. While the former are conceptual objects with external semantics, i.e., with reference to facts, the latter refer to ideal objects with internal semantics and in which the correspondence is sought through reason, what we will refer to as thought correction.
Thus, the ultimate task of modelers in interdisciplinary teams is to obtain, from the model, propositions derived by correct arguments, which, when interpreted and in the form of statements, will not only be valid, but also aspire to be true.
EPISTEMOLOGICAL DIFFERENTIATION
Regarding the millenary dispute of whether reason or experience are the genesis of our knowledge regarding the world, modelers in interdisciplinary contexts will have to build some clarity for the purposes of the coexistence that they will have to maintain between the methods of their discipline and the classic ones of the factual sciences. For example, in the hypothetical-deductive method that assumes the flow in large blocks: observation; hypothesis; and testable consequences, where is the contribution of a mathematical modeling located? Having some light is a need that will arise in the interdisciplinary interaction, which will probably be present when defining the roles and evaluating the scope of the formalist contribution.
In the factual sciences, the researchers are interested in consolidating or innovating in answers to certain research questions and, based on the analysis of previous observations, raising hypotheses, i.e., conjectures about context-causes-effects that explain the phenomena of interest. The hypotheses are normally tested through the implementation of specific experimental designs. What does a model do before a hypothesis? Can a mathematical model reject or accept a hypothesis? Do derived mathematical propositions clearly have, by interpretation, real reports as statements about reality?
With respect to the contrasts, we read: “In the hypothetical-deductive method, the contrasts should be experimental. In addition, they should be robust, in the sense that they should tell us clearly whether the consequences deduced from the hypothesis occur in reality or not” (Sobre un concepto histórico de ciencia [On a historical concept of science], Carlos Pérez).
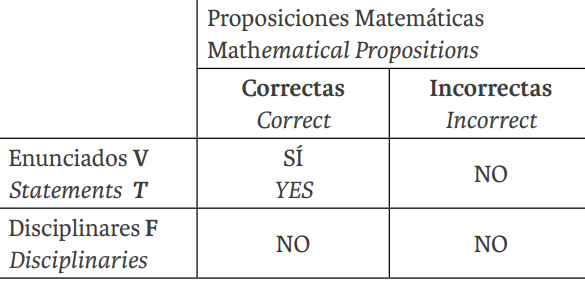
As already observed, the theoretical projective field (the disciplinary) and the mathematical field concur in the work of interdisciplinary teams. It is worth noting that a scientific hypothesis is a statement of the context field. This way, it is not a fact and, in principle, neither is it a mathematical proposition; it is only linked to the facts by reference. Therefore, entering the field of truth, we observe that it is in this disciplinary field where the statements can be true or false, since in the reality field, these qualifiers do not make sense, because the facts occur or not.
Now, regarding the field of mathematics, it is better to consider other terms, since for group communication it is prudent to refer to propositions, highlighting those that have a demonstration, to distinguish between correct or incorrect deductive thought. Thus, what is desired is to reach hypothetical statements that have a mathematical correlate as correct propositions in the passage from the antecedent to the consequent and, furthermore, when interpreted, theypass the empirical tests or contrasts in order to become true. However, the latter is based on resisting a permanent test of non-falsity in the experimental field.
It is worth noting that a hypothesis is a reality bet. It is that statement with some degree of foundation and, furthermore, testable. Presupposing certain facts, it affirms that another fact necessarily follows, generally related to the specification for a perceived object of a state or a type of state within the feasible ones. Therefore, although the theoretical projective field tells us about empirical contrast through experimentation, there is also the rationality contrast, i.e., where a first opportunity for mathematical modeling arises, testing whether a hypothesis is logically consistent.
Another possibility is modeling the empirical tests (i.e., not possible to be implemented), as mental experiments, checking that their analytical conclusions go (they admit the semantic interpretation) in the direction of what the hypothesis affirms. However, a statement like a hypothesis, with its generality, even being logically consistent, can become a less plausible statement, one is never sure whether an experiment that contradicts it will appear. Thus, since the truth of a consistent hypothesis risks its plausibility in empirical control, lowering the expectations, the models only add or subtract arguments
or support for their formulation.
Mono-disciplinary scientific teams usually structure or guide their work plan through a research question, and the same fact occurs in interdisciplinary teams. What type of model is appropriate for this question? What are the legitimate transfers from what is represented to the representative model (abstraction), and vice-versa (interpretation)? What are the minimum, first and necessary elements to consider, in order to build a model with some analogical claims regarding phenomena of reality with possibilities of contributing with an answer to the research question? It is worth being clear about the ontological distinction between objects and facts of reality, language as an articulator of concepts through propositions, and the set of ideal objects and formal relationships, the mathematical propositions that aspire to become a model.
CONCLUSION
When modeling, we should not only be aware of the differences between context and mathematics regarding objects, declarative propositions, and methods involved. There are many other aspects with philosophical traces that modelers can explore for a better understanding of their work. An enormous space tempts the exploratory desire; it is the sense of value that involves the tasks, be it of use and, why not, also the aesthetic one; however, this editorial has already gone on too long.
I end by pointing out that, in the face of a research question, its associated hypothesis and the level of precision of the answer, apart from what has already been stated, it is useful and beautiful that the modelers aspire to constructions that perform the task in the simplest possible way. For the present and other topics, it is worth recommending the book “Deja a la estructura hablar: Modelización y análisis de sistemas naturales, sociales y socioecológicos” (Let the structure speak: Modeling and analysis of natural, social and socioecological systems) by Dr. Rodrigo Ramos.
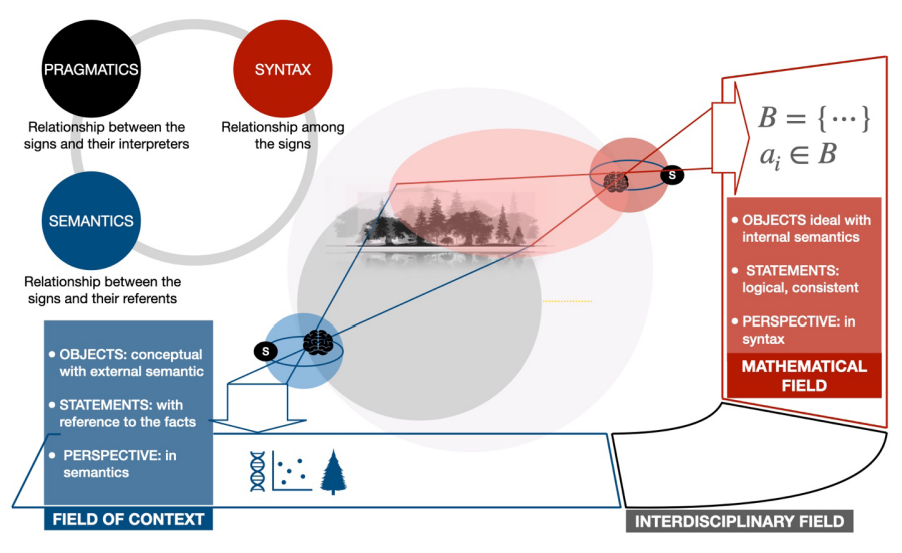
Figure 3. At the field of context, the statement has significance in the facts. Its semantics is external; it occurs or not in its real referents. On the other hand, in mathematical propositions, the referents are only concepts, ideal objects, internal semantics; syntax and the relationship among the signs are highlighted. The interaction defines, by adaptation, the interdisciplinary field of communication in which statements of context and mathematical propositions coexist. Regarding pragmatics, the third semiotic vertex, it is the concern of other imaginable fields, e. g., those related to psychology or educational sciences.